字符串算法之 KMP
Substring Search 的简要历史
子字符串查找研究的问题是:给定一个字符串 S(假设长度为 M) 和一个目标查找子串 P(长度为 N),找出 S 中 P 出现的位置。同时算法可以延伸到找出 S 中 P 出现的所有位置,出现的次数等。

子串查找算法的历史发展是从暴力破解法(Brute-force Substring Search)开始的,这个直接的解法在最差情况下是 MN 运行时。在 1970 年, S. Cook 提出一个优化的理论结果值,指出子串查找可以在(M+N)运行时下解决。直到 1976,Knuth, Morris, and Pratt 才发布他们的 KMP 算法。同时 R. S. Boyer and J. S. Moore 也发表他们的解法。他们的算法都能做到 M+N 的运行时,但是都较难理解(据说有一无名系统程序员觉得 Moore’s 算法太难理解而宁愿采用暴力破解法)。到 1980 年,M. O. Rabin and R. M. Karp 发现了一种和暴力破解一样易懂但能做到 M+N 运行时的算法,虽然会利用到 hashing。
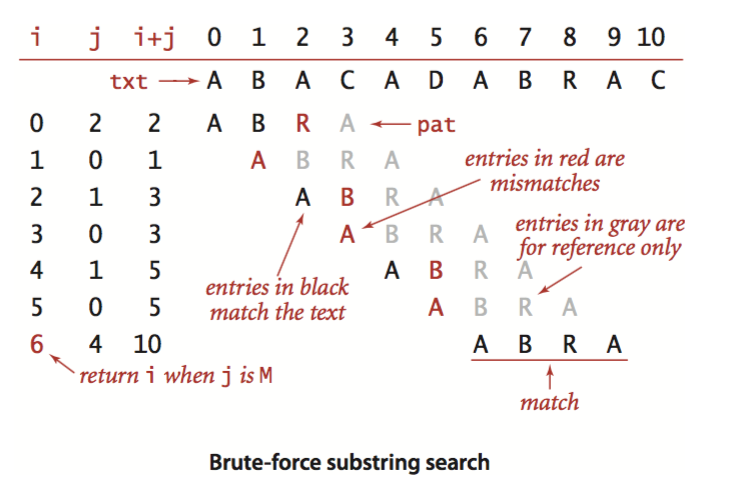
Brute-force substring search
暴力破解的思路是这样的:从字符串的左边第一个字符开始,和目标子串的左边第一个字符匹配,如何发现是匹配,那么被查找串和目标串的查找下标都右移动一位,变成 1(假设下标从0开始),然后匹配。如果发现不匹配,那么被查子串的匹配下标向右移动,但是目标子串下标回到0,也就是重新开始匹配。以此类推,直到目标子串的匹配下标移动到最后一个字符,那么就算找到匹配;或者被查字符串的匹配下标先移动到最后一个字符,那么就是没有找到匹配。
下图是暴利匹配的步骤图。一旦发现不匹配,那么目标子串的被查下标就回撤到0,而被查字符串的匹配下标仅向后移动一位。所以在最坏情况下,此算法消耗 MN 运行时,这是在匹配总是在最后一个字符失败的情况下达到。
KMP 算法要点
暴力破解的问题在于低效的回撤策略。KMP 则从已经匹配的字符串中提取信息,做到在不匹配发生时候,被查下标不需要回撤到0。那么如何做到有效回撤呢?假设如下被查字符串和目标子串分别如下:
S: abcabdabcabdabcabdabdabc
P: abcabdabc
KMP 算法涉及到两部分:
- 预处理(preprocessing),构建 Partial Match Table
- 查找,使用构建好的 Partial Match Table 来做到有效回撤
什么是 Partial Match Table
在字符串中,前缀串集(set of proper prefixes)是除了最后一个字符外的所有字符可以组合成的连续子串的集合,而且必须包含第一个字符;后缀串集合(set of proper suffixes)是除了首个字符外的所有字符可以组合成的连续子串的集合,而且必须包含最后一个字符。
最长前后缀匹配串(longest prefix/suffix match)是在前缀串集合和后缀串集合中,最长的那个子串。给定一个字符串 abcabdabc,它的所有子串和对应的最长前后缀匹配串是:
a: 没有匹配
ab: prefixs: [a]
suffixes: [b]
-
abc: prefixs: [a,ab]
suffixes: [bc, c]
-
abca: prefixs: [a,ab,abc],
suffixes: [bca,ca,a]
a
abcab: prefixs: [a,ab,abc,abca]
suffixes: [bcab,cab,ab,b]
ab
abcabd: prefixs: [a,ab,abc,abca,abcab]
suffixes: [bcabd,cabd,abd,bd,d]
-
abcabda: prefixs: [a,ab,abc,abca,abcab,abcabd]
suffixes: [bcabda,cabda,abda,bda,da,a]
a
abcabdab: prefixs: [a,ab,abc,abca,abcab,abcabd,abcabda]
suffixes: [bcabdab,cabdab,abdab,bdab,dab,ab,b]
ab
abcabdabc: prefixs: [a,ab,abc,abca,abcab,abcabd,abcabda]
suffixes: [bcabdabc,cabdabc,abdabc,bdabc,dabc,abc,bc,c]
abc
Partial Match Table 的概念就是找出字符串中所有子串的最长前后缀匹配串的长度的数组。因此根据上面的分析,字符串 abcabdabc 的 Partial Match Table 如下。在这里下标 i 的数值指的是 0..(i-1) 子串的最长前后缀匹配串的长度,所以 i = 4 是 tb[4] = 1。
i: 0 1 2 3 4 5 6 7 8
P: a b c a b d a b c
tb[i]: -1 0 0 0 1 2 0 1 2 3
以下是 Partial Match Table 的 C 语言实现。在这里第一个字符的 longest prefix/suffix match 默认设为 -1。
1
2
3
4
5
6
7
8
9
10
11
12
13
void partialMatchTable(char *ptn, int ptn_size, int *tb){
int i = 0;
int j = -1;
tb[i] = j;
while(i<ptn_size){
while(j>=0 && (ptn[i] != ptn[j])){
j = tb[j];
}
i = i+1;
j = j+1;
tb[i] = j;
}
}
从 0..ptn_size 来做循环,循环的细节如下:
- i = 0, j = -1 ,开始循环,但不满足内循环的条件,运行 9 到 11 行代码设 i = 1, j = 0, tb[1] = 0;
- i = 1, j = 0, 因为 ptn[1] != ptn[0],进入内循环设 j = tb[0] = -1,之后不满足进入内循环的条件,运行 9 到 11 行代码,设 i = 2, j = 0, tb[2] = 0;
- i = 2, j = 0, 因为 ptn[2] != ptn[0],进入内循环设 j = tb[0] = -1,之后不满足进入内循环的条件,运行 9 到 11 行代码,设 i = 3, j = 0, tb[3] = 0;
- i = 3, j = 0, 因为 ptn[3] == ptn[0,运行 9 到 11 行代码,设 i = 4, j = 1, tb[4] = 1;
- i = 4, j = 1, 因为 ptn[4] == ptn[1],运行 9 到 11 行代码,设 i = 5, j = 2, tb[5] = 2;
- i = 5, j = 2, 因为 ptn[5] != ptn[2],进入内循环设 j = tb[2] = 0,再循环设置 进入内循环设 j = tb[0] = -1 退出循环运行 9 到 11 行代码,设 i = 6, j = 0, tb[6] = 0;
- … 依此类推直到字符串尾
在这里当 i = 5 是出现了不匹配,那么 j 该如何设值就是关键。首先通过之前的计算,我们已经知道在 5 之前的字符串已经有 2 字符的长度的匹配,那么在这两字符中间,有可能有字符会与 i 匹配,所以要将 j 的下标变为 tb[2],也就是 0,然后通过对比 ptn[0] 和 ptn[5]。如果匹配,则设置 tb[i],如果不匹配,则继续把 j 向前移动,直到 -1。
通过考察以下典型字符串,则上面的算法会更好理解。此处省略详细过程,感兴趣可以查看视频。
Partial Match Table
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0
a c a c a b a c a c a b a c a c a c a c
-1 0 0 1 2 3 0 1 2 3 4 5 6 7 8 9 10 11 4 5 4
查找
有了 Partial Match Table 后,查找算法如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <stdlib.h>
#include <stdio.h>
#include <string.h>
// 此处省略 partialMatchTable 算法
void kmp(char *ptn, char *str){
int ptn_size = (unsigned int)strlen(ptn);
int tb[ptn_size+1];
partialMatchTable(ptn, ptn_size, tb);
int str_size = (unsigned int)(strlen)(str);
int i = 0;
int j = 0;
while(i<str_size){
while(j>=0 && (str[i] != ptn[j])){
j = tb[j];
}
i = i+1;
j = j+1;
if(j==ptn_size){
printf("pattern match at index %i\n", i-ptn_size);
j = tb[j];
}
}
}
int main(){
char str[] = "abxabyabmabxabyabzababc";
char ptn[] = "abxabyabzab";
kmp(ptn, str);
return 1;
}
分步来看查找算法。
- i = 0..7,j = 0..7 之间时,被查串和目标串都匹配,则 i 和 j 按照 1 来递增;
- i = 8, j = 8 是不匹配,则通过 partialMatchTable 来确定 j 的值,这个时候可以找到下一个最长匹配串的长度,也就是 tb[8] = 2,然后用 ptn[2] 和 str[8] 比较
- ptn[2] != str[8],则继续计算 j = tb[2] = 0
- ptn[0] != str[8],则继续计算 j = tb[0] = -1,退出循环
- i = 9, j = 0,继续进行匹配
- … 省略其他步骤解释
Partial Match Table
0 1 2 3 4 5 6 7 8 9 0 1
a b x a b y a b z a b
-1 0 0 0 1 2 0 1 2 0 1 2
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2
a b x a b y a b m a b x a b y a b z a b a b c
a b x a b y a b z a b
|---> unmatch, current i = 8, j = 8, set j = tb[8] = 2
a b x a b y a b z a b
|---> unmatch, current i = 8, j = 2, set j = tb[2] = 0
a b x a b y a b z a b
|---> unmatch, current i = 8, j = 0, set j = tb[0] = -1, end while loop. Then i++, j++
0 1 2 3 4 5 6 7 8 9 0 1 2 3 4 5 6 7 8 9 0 1 2
a b x a b y a b m a b x a b y a b z a b a b c
a b x a b y a b z a b
|---> match found, print and set j = tb[11] = 2
a b x a b y a b z a b
|---> curent i = 20, j = 2, (str[i] = a) != (ptn[j] = x)
小结
KMP 算法在理解上并不困难,但是难点在于实现 partial match table 和最终的查找算法,关键点在于不匹配出现的时候,如何重置目标串的当前查找下标。KMP 的算法运行时是 M+N。
学习链接和参考资料