Cycle Detection

#Cycle Detection

问题

给定这样一个问题，怎么解？ > Directed cycle detection. Does a given digraph have a directed cycle? If so, find the vertices on some such cycle, in order from some vertex back to itself.

问题是给定一个有向图，请问图中是否有环？如果有，请打印路径。假定给出下图中左边有向图，求解此图是否有圈。当然下图太简单，一看就能看出来一个有圈。但如果换成右图，就不是那么直接了。

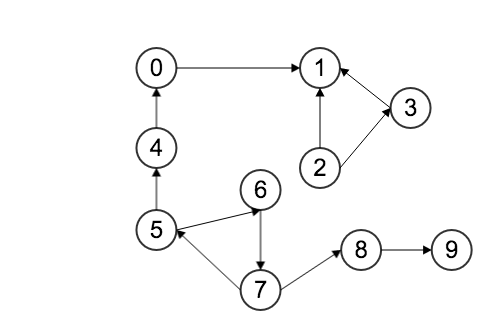
10 个 vertexs 的有向图

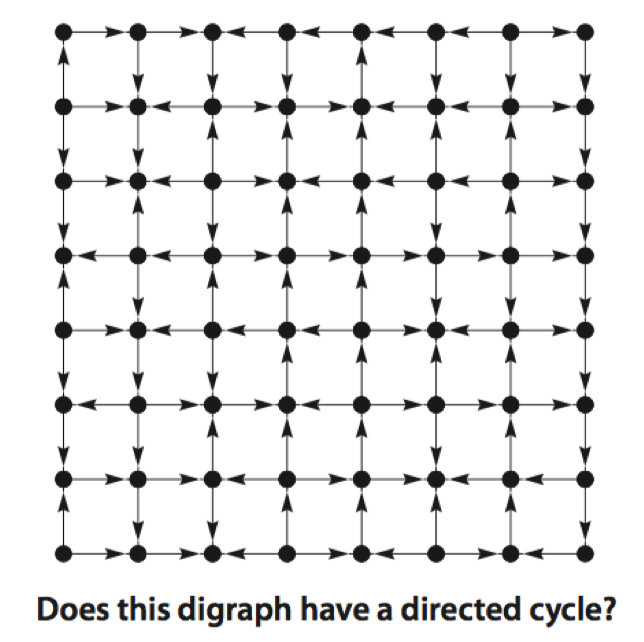
略复杂的有向图[1]

解题思路

一旦涉及到图的问题，不是上 DFS (深度优先搜索) 就是 BFS (广度优先搜索)。这里的问题明显的深度优先处理，对每一条可能的路径做有无圈的检测。

首先是要遍历所有的点，从 0 到终点，对其作 DFS。因为如上图中的结构，如果把 0 作为原点，则不会检测到圈。只有在遍历到节点 5，并作为原点的时候，才会发现圈 7 -> 5 -> 6 -> 7。
同时在处理某一条路径到时候，标记访问过程中碰到的点。如某个邻居点(adjacent node)已经被标记为访问（marked)，则跳过；反之在该临点上调用 dfs，进入递归，直到到达路径的结束点。如当把节点 5 作为原点时，由于 4 是已经访问过了，由此可以跳过对 4 的遍历，对 6 开始遍历。
那么如何探测圈呢？答案是需要一个存储途经点的结构 onStack，一旦新的临点已经在这个结构中了，则说明是‘撞墙路’，也就是圈。比如说在从 5 开始，向 6 走的时候，把 5 和 6 加入 onStack 中。然后 6 到 7，由于 7 不在结构中，加入，同时向下走。在 7 指向 6 的时候，发现 6 已经在 onStack 了，则认为检测到了圈。但如果在结束当前 recursive stack 的时候没有发现圈，则应该反标记一路上遇到的点，不再把它们看为成为圈的因子。

总结以上分析，检测算法需要如下数据结构和变量：

stack：堆，基础数据结构，FIFO，支持 push, pop, isEmpty 和 top
directed graph：有向图，基础数据结构，支持 addEdge, print
marked：所有点的访问情况。一组 V(图中 vertex 的个数) 个 boolean 元素的数组
edgeTo：递归途中碰到的所有边。一组 V 个整数元素的数组，如 edgeTo[1] = 0 代表从 0 可以到 1。
onStack：一组 V(图中 vertex 的个数) 个 boolean 元素的数组

实现

下面是 C 的实现。首先是 main 函数。其中 graph 的创建省略。

1
2
3
4 int main(){
  Graph* graph = creatGraph();
  detectCycle(graph);
}

然后到 detectCycle 方法。

1
2
3
4
5
6
7
8
9
10 void detectCycle(Graph* graph){
  // createBooleanArray 创建 V 个元素的 boolean 数组，V = 图中点个数
  bool* marked = createBooleanArray(graph->V);
  int* edgeTo = malloc(graph->V*(sizeof(int)));
  bool* onStack = createBooleanArray(graph->V);
  Stack* cycle = NULL;
  // 从 0 开始作为原点，遍历
  for(int pivot =0; pivot< graph->V; pivot++)
    dfs(graph, pivot, marked, edgeTo, onStack, cycle);
};

dfs 方法的关键点在于循环中的检测。如果检测到该临点点已经访问过(marked[point] = true)，则不处理。如果检测到临点已经在路线中，则认为检测到圈（onStack[point] = true)，生成圈(cycle)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31 void dfs(Graph* graph, int pivot, bool* marked, int* edgeTo, 
  bool* onStack, Stack* cycle){
  marked[pivot] = true;
  onStack[pivot] = true;
  AdjListNode* adjListNode = graph->array[pivot].head;
  while(adjListNode){
    if(cycle){
      return;
    }else if(!marked[adjListNode->dest]){
      // 如果当前的邻居是第一次到达，则建立 pivot 和 邻居之间的关联, 同时对邻居开始做 recursive
      edgeTo[adjListNode->dest] = pivot;
      dfs(graph, adjListNode->dest, marked, edgeTo, onStack);
    }else if(onStack[adjListNode->dest]){
      // 当前邻居已经到过了，那么就去判断这个邻居是不是在 stack 上，如果在，则说明形成了环路
      printf("--- cycle detected. ---\n");
      cycle = StackCreate();
      for(int x = pivot; x != adjListNode->dest; x=edgeTo[x])
        StackPush(cycle, x);
      StackPush(cycle, adjListNode->dest);
      StackPush(cycle, pivot);
      while(!IsEmpty(cycle)){
        printf("->%i ", StackTop(cycle));
        StackPop(cycle);
      }
      printf("\n");
    }
    adjListNode = adjListNode->next; // 指向下一个邻居
  }
  // 所有的邻居都处理完了，则也就是这个节点开始的对邻居的遍历也结束了，那么这个点就不在 stack 上了
  onStack[pivot] = false;
};

下面这张图[2]是演示递归的过程。这里发现的圈是 3 -> 5 -> 4 ->3。

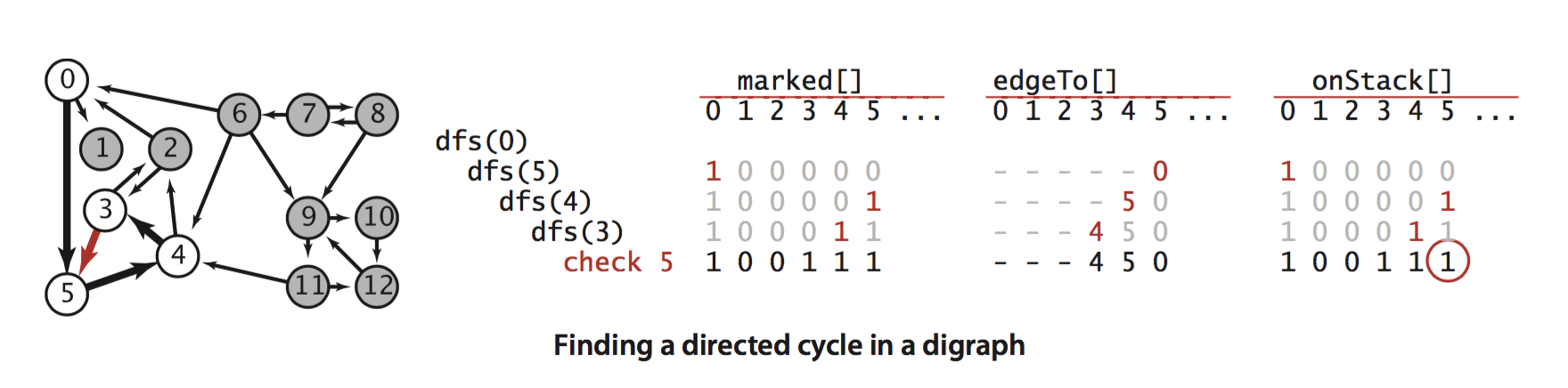
再看实现

其实以上的实现会把图中所有的圈都找出来。但如果希望检测到圈就停止，该怎么办？

<未完>